近日，浙江师范大学数理医学院罗守胜副教授团队在数学建模和数值计算领域权威期刊Applied Mathematical Modelling上发表高水平研究论文“A Binary Characterization Method for Shape Convexity and Applications”。副教授罗守胜为第一作者，浙江师范大学为第一完成单位。该工作得到了国家自然科学基金、香港浸会大学内部研究资助等重点项目支持。

形状先验广泛应用于图像处理和计算机视觉等领域。图像分割是医学图像处理中的重要研究内容，也是辅助诊断的基础。虽然图像分割方法成果丰富，然而在分割强噪声、光照偏差和弱对比度图像时表现不佳。因此，结合形状先验的图像分割（如星形、凸性和连通性）受到越来越多关注，形状先验的可计算刻画方法是基于形状先验的图像分割方法的核心与基础。形状凸性是重要的形状先验之一。

当前凸性建模方法可分为两大类：区域方法和边界方法，但二者均存在局限性：1. 区域方法直接利用凸性的数学定义（即任意两点连线仍在区域内部），通过构造二值指示函数并惩罚违反凸性结构的像素配置来保证区域的凸性。然而，该类方法需在多方向上枚举可能的像素对，导致计算复杂度高，优化问题通常为NP难。2. 边界方法基于区域边界的曲率信息对凸性进行刻画，常通过显式或隐式函数（如曲线

函数或距离函数）估算边界曲率。尽管该方法具有较强的几何解释力，但其优化目标涉及非线性和非凸约束，依赖高阶导数的数值计算，导致收敛慢、算法不稳定，尤其在图像含噪或边界模糊时效果不佳。

本文主要研究了融合凸性的图像分割方法，提出了新的凸性刻画方法，设计了高效的算法，并应用于图像分割、凸包计算等领域。核心思路是使用二值指示函数替代传统的水平集函数计算目标边界的曲率，并将目标凸性等价于该指示函数的二次函数的非负性约束，显著简化模型复杂性，有利于设计高效求解算法。基于此，本文通过引入线性化策略，采用邻近交替方向乘子法（Proximal ADMM）求解（多）凸目标分割模型。图1、图2，图3分别展示了单目标、多目标和环形目标的分割结果，这些实验结果表明本文方法有较强的鲁棒性与稳定性，在性能与稳定性方面优于现有方法。

算法1: Proximal ADMM 求解线性化的多凸目标分割模型（内循环）

算法2: 线性化多凸目标分割模型（外循环）

图1 不同方法的单目标分割结果比较

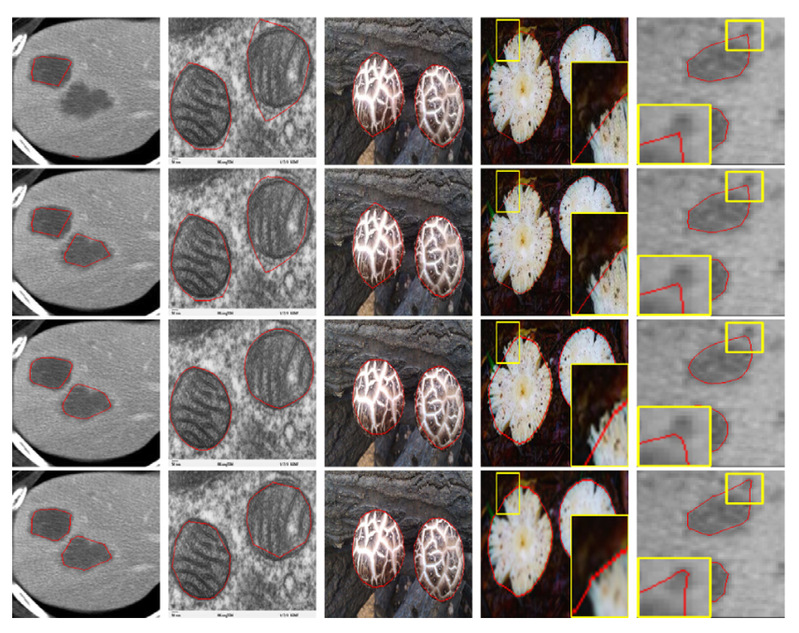
图2 不同方法的多目标分割结果比较

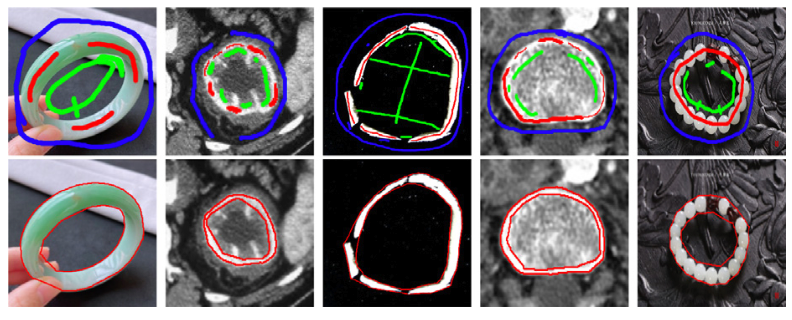
图3 凸环分割结果